Chapter 1 The Beauty of Geometry

You'll find this Japanese geometry challenge quite delightful.

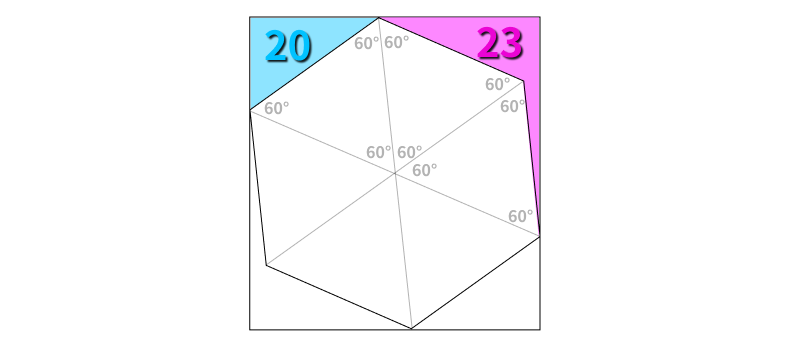
A regular hexagon is inscribed within a rectangle, which creates a triangle with an area of 20 cm² and a quadrilateral with an area of 23 cm². The task is to determine the area of the hexagon.

This intriguing problem was presented during the Preliminary Round of the 2023 Japan Mathematical Olympiad.

Where do we begin?

As is often the case in geometry, the trick lies in adding one or two lines at just the right spots.

Since we know that the hexagon is regular, it might be beneficial to divide it into six equilateral triangles.

However, the crucial line—depicted as a blue dashed line below—turns out to be the one that reveals the entire solution.

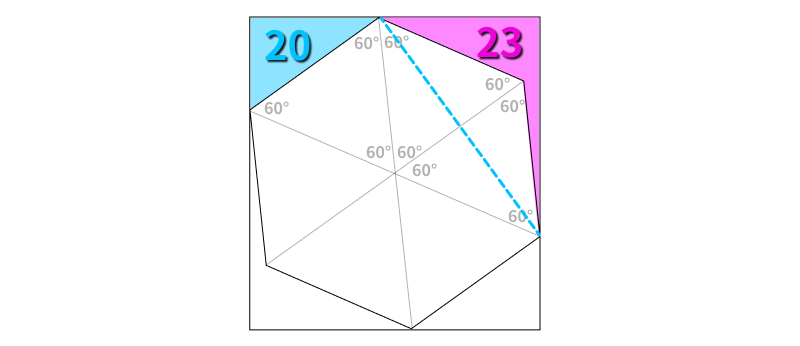
Why is this blue dashed line so significant?

It bisects one of the equilateral triangles in the hexagon, forming a 90° angle with the hexagon's edge. Next, consider the right triangle formed with the top and right edges of the rectangle (highlighted in light blue).

We can observe that this triangle shares an angle (marked as ?) with the smaller blue triangle, which has an area of 20. Since both triangles are right triangles, we can deduce that they are similar.

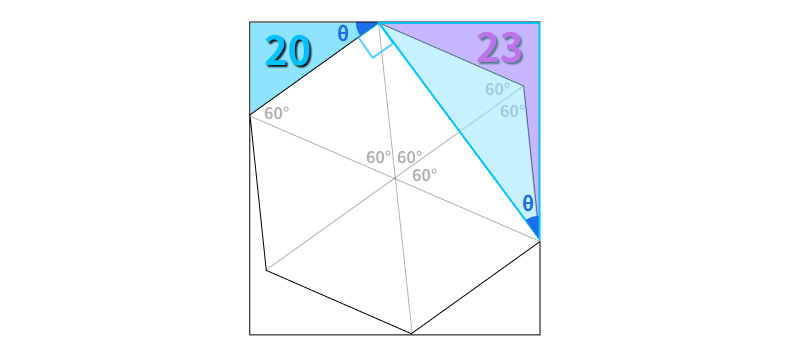
Understanding that the two blue triangles are similar leads us to find the ratio of their side lengths.

This can be easily calculated by examining the 30°–60°–90° triangle illustrated in orange below.

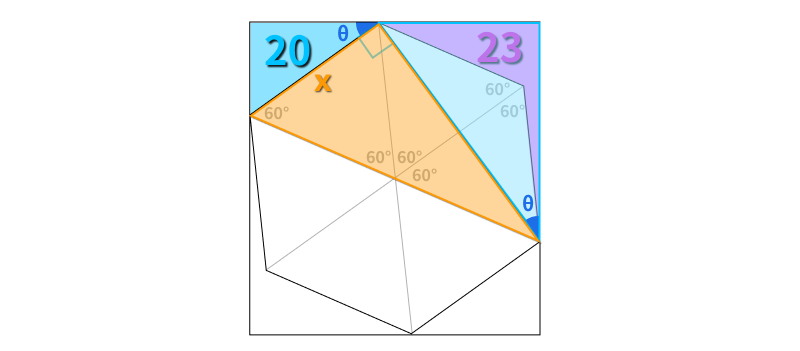
If we denote the side length of the hexagon as x, then the hypotenuse of the orange triangle will measure 2x, while the other side will be √3x. This establishes that the ratio between the corresponding sides of the blue similar triangles is √3 : 1.

Consequently, the area of the larger blue triangle must be three times that of the smaller blue triangle. Since the area of the smaller blue triangle is 20, the area of the larger blue triangle can be calculated as 3 × 20 = 60. We can also express this area as 23 plus the area of one of the equilateral triangles.

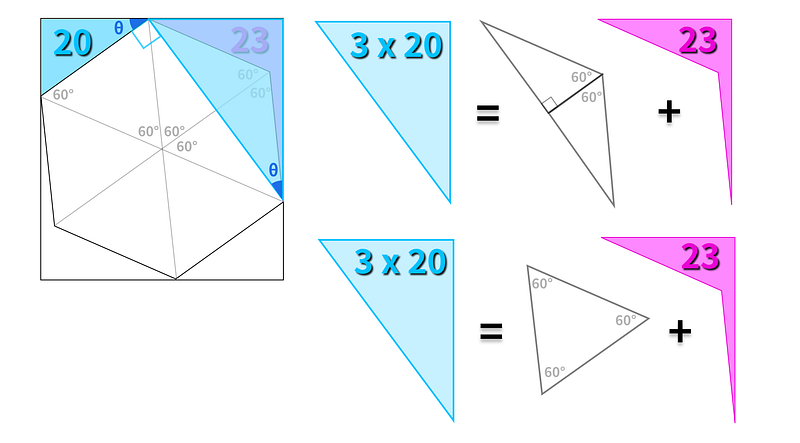
This means that the area of one of the equilateral triangles must be 60 - 23 = 37. Thus, the total area of the hexagon is 6 × 37 = 222 square units.

I told you it was a charming problem!

Chapter 2 Exploring Further with Videos

The first video, titled "A Japanese Temple Problem, a Sangaku," delves into the beauty of mathematical challenges inspired by Japanese culture. This video explores similar geometric concepts and offers insights into solving them.

The second video, "A Geometry Problem Inspired by Japanese Sangaku," further enhances understanding by presenting various geometric problems, enriching the viewer's appreciation for the elegance of mathematics.