Exploring the Concurrency of Lines in Triangle Geometry
Written on
Chapter 1: Understanding Triangle Geometry
In this section, we analyze a problem from the 2010 Indonesia National Olympiad focusing on an acute triangle ABC, where the side AC is longer than BC. The circumcenter of triangle ABC is designated as point O. The altitude from point C meets line AB and the circumcircle at points D and E, respectively. A line that runs through O, parallel to AB, intersects AC at point F. The objective is to demonstrate that the lines CO, the line through F that is perpendicular to AC, and the line through E that is parallel to DO all meet at a single point.

To facilitate our understanding, let’s utilize the Theorem Grid to reference the various theorems employed in this proof.
Introducing: The Theorem Grid
Theorems on Geoclid So Far
Section 1.1: Proof Development
Let M represent the midpoint of segment CA, while g is defined as the line that runs parallel to AB and passes through points O and F. We will assume that the line through F, which is perpendicular to AC, intersects the line CO at point T. To validate our claim, it is sufficient to demonstrate that TE is congruent to OD. Given that angle CDA equals 90°, and M is the midpoint of CA, we can apply Theorem 1.11 to draw our conclusions.
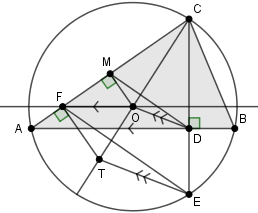
Since angle CDA equals 90° and g is parallel to DA, it follows that g is perpendicular to CE. Additionally, since OC and OE are radii of the circumcircle (which implies that triangle OCE is isosceles), we can invoke Theorem 1.2, establishing that g serves as the perpendicular bisector of CE. By the same theorem, triangle FCE is also isosceles, leading us to conclude that FC is equal to FE.
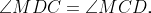
By combining angle MDC with angle MCD and utilizing Theorem 1.1, we arrive at the conclusion that angle CMD equals angle CFE, thus yielding MD equal to FE.
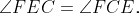
The next steps are straightforward. Applying Theorem 1.1 again, we find that angle CMO equals angle CFT, leading us to infer that angles CMD and CFE are equal. From this, we gather that angles OMD and TFE must also be equal. Consequently, the ratios MD/FE and MO/FT yield the same proportion, affirming that MO/FT equals MD/FE. Bringing these results together with Theorem 1.1, we can assert that angle OMD equals angle TFE. Since these angles are equal and MD is congruent to FE, we can invoke Theorem 1.1 one final time to prove that TE is congruent to OD.
We have completed the proof.
Endnote
You may be curious about the role of the triangle's acuteness in our proof. Interestingly, this property is not essential. It is possible to follow a similar reasoning to confirm the validity of the proof even if triangle ABC is obtuse (can you imagine how?). In this case, points F and T would lie outside the circumcircle.
If you appreciate this content and wish to support my writing endeavors, consider becoming a member. For just $5 a month, you'll gain unlimited access to all my stories on Medium. Signing up through my link allows me to earn a small commission.
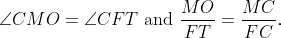
Chapter 2: Supplemental Video Insights
To deepen your understanding, check out the following videos that explore related geometry concepts.
The first video titled "Olympiad Geometry Problem #95: IMO 2010 #2 - YouTube" offers an insightful analysis of a similar geometrical problem. This video can enhance your grasp of the core principles involved.
The second video, "Indonesia Math Olympiad Question | You should be able to solve this! - YouTube," presents a challenge that aligns closely with our topic, encouraging you to apply what you've learned.