Unlocking the Secrets of Inverse Problems: A Mathematical Journey
Written on
Chapter 1: Introduction to Inverse Problems
Imagine stepping into the shoes of a detective navigating a landscape filled with numbers and equations, ready to embark on an exciting quest to decipher one of the universe's captivating enigmas. This adventure leads us into the intricate domain of Inverse Robin Problems—a challenging yet fascinating subject that, despite its complexity, is essential for grasping the nuances of our world and beyond. Recent advancements in this field illuminate the path forward, making it easier to digest these concepts as we delve deeper.
Section 1.1: Defining Inverse Problems
To appreciate the importance of Inverse Robin Problems, it’s vital to first clarify what inverse problems entail. Picture a situation where you can observe the effects of an unknown process, but must deduce the underlying cause. It’s akin to glimpsing shadows on a wall and attempting to infer the shapes of the objects that cast them. In scientific contexts, such problems are commonplace—particularly in medical imaging, where physicians interpret scan results to understand internal conditions, or in astronomy, where researchers analyze light from distant stars to ascertain their compositions.
Subsection 1.1.1: The Robin Boundary Condition
In mathematics and physics, boundaries serve as the limits of scenarios or conditions, much like the edges of a jigsaw puzzle. The Robin Boundary Condition is a unique type of boundary condition utilized in mathematical equations to characterize how a variable behaves at the surface of an object. This is comparable to establishing guidelines for how heat or sound propagates through various materials.
Section 1.2: The Importance of Inverse Robin Problems
The Inverse Robin Problem focuses on determining unknown boundary conditions based on available information. Tackling these problems is vital for numerous practical applications. For example, in engineering, it aids in identifying material properties based on their reactions under specific conditions. In geophysics, it plays a crucial role in understanding subsurface structures, which is essential for oil exploration and assessing earthquake risks.
Chapter 2: The Bayesian Approach
Here, the Bayesian method comes into play. Named after Reverend Thomas Bayes, this technique revolves around utilizing probability to formulate educated guesses, which are subsequently refined as more data becomes available. In the context of inverse problems, this involves making initial assumptions about unknown boundary conditions and adjusting them as further data is collected. The beauty of this method lies in its flexibility; it continuously evolves and enhances with each new piece of information.
To visualize how the Bayesian method operates within Inverse Robin Problems, consider the graph below, which depicts the iterative process of refining estimates—similar to how a detective narrows down a list of suspects by progressively honing in on the truth.
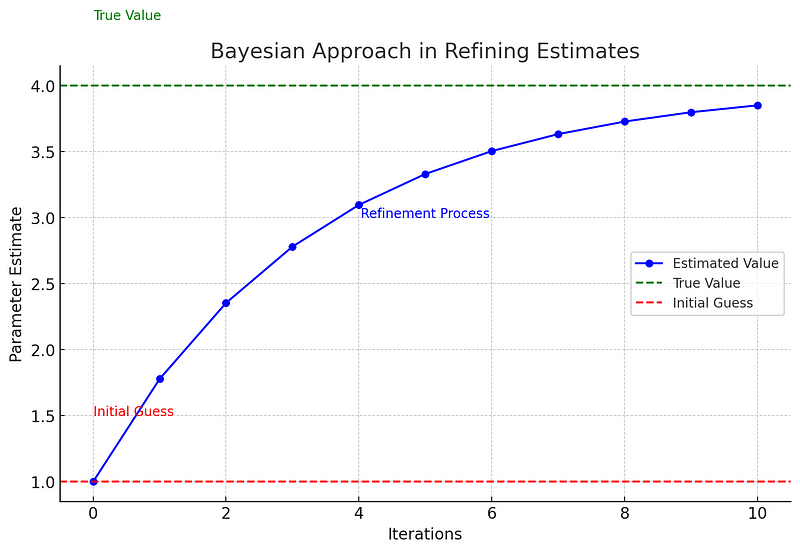
This graph illustrates the Bayesian refinement procedure applied to Inverse Robin Problems, beginning with an initial estimate (red line) and gradually converging towards the actual value (green dashed line) through iterative updates (blue dots). Each iteration symbolizes a step closer to solving the enigma, akin to a detective assembling clues to crack a case.
Chapter 3: The Role of Mathematics
Mathematics transcends mere numbers and equations; it serves as the language through which we communicate with the universe. In the realm of inverse problems, mathematics acts as the detective’s toolkit, aiding in the discovery of concealed mysteries. The Bayesian method relies heavily on intricate mathematical formulas and computations to interpret data and extract significant insights.
Section 3.1: Real-World Applications
The real-world implications of resolving Inverse Robin Problems are extensive and diverse. In healthcare, they enhance modalities like MRI and CT scans, yielding clearer and more precise images. In environmental science, these solutions facilitate the assessment of soil characteristics and underground water flow, crucial for sustainable agriculture and water management. They are also critical in engineering, contributing to the design and testing of new materials and structures, ultimately leading to safer and more efficient construction practices.
Section 3.2: Challenges and Advancements
While the Bayesian approach offers a solid framework for addressing these complex problems, it is not without challenges. The primary difficulty lies in managing vast amounts of intricate data and ensuring the accuracy of predictions. This requires advanced computational techniques and algorithms, alongside a continuous cycle of model refinement and validation.
Conclusion: The Future of Inverse Problems
Although the study of Inverse Robin Problems and the Bayesian approach may appear abstract, their applications are strikingly relevant and impactful across various scientific and engineering disciplines. As we continue to expand the horizons of human knowledge, methodologies like the Bayesian approach provide us with powerful tools to decode the enigmas concealed within the complex equations that define our universe.
Through our exploration of Inverse Robin Problems and the Bayesian approach, we've gained insight into a fascinating and critical area of scientific inquiry. This journey underscores how contemporary scientific challenges are being addressed with innovative mathematical tools, enhancing our understanding of the world and our capacity to navigate its myriad mysteries.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your portal to the future of technology. Subscribe for new insightful videos every Saturday!
Watch us on YouTube
This video, "Oracy in the Classroom: Strategies for Effective Talk," explores various techniques to enhance communication and collaboration in educational settings, providing valuable insights for teachers and students alike.