Chapter 1: Introduction to the Erdős Distance Problem

The Erdős Distance Problem is a significant topic in the realm of geometry, attributed to one of the most influential mathematicians in history, Paul Erdős. He regarded this problem as one of his notable contributions to mathematics. In this overview, we will explore the intricacies of the problem and what is currently understood about it.

The Erdős Distance Problem is notable for being both easy to describe and a subject of active research across various mathematical disciplines. Unlike more complex problems such as the Hodge Conjecture, which are challenging to articulate, the Erdős Distance Problem remains accessible and is being investigated through various mathematical frameworks, including combinatorial geometry and optimization.

The core of the problem can be summarized as follows: What is the minimum number of distinct distances that can be formed from a set of n points? Let's begin our analysis in a two-dimensional plane (ℝ²).

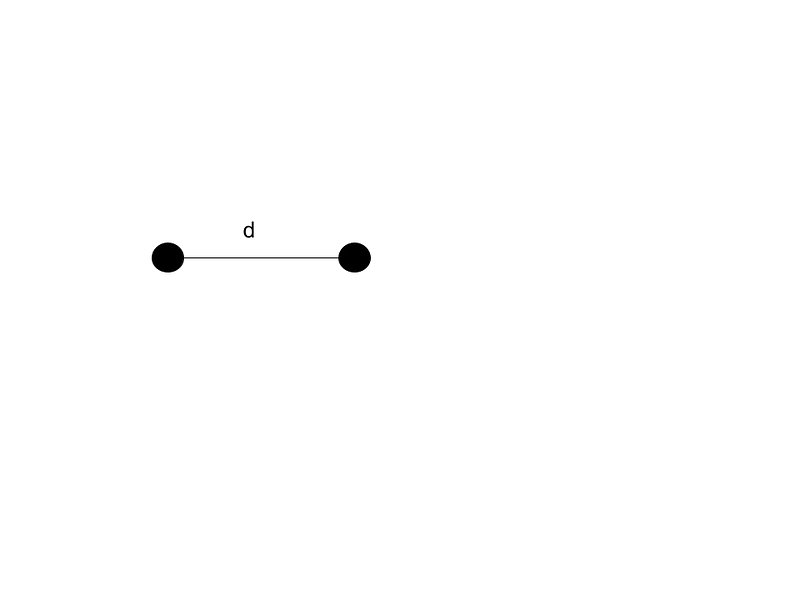
If we have a single point, the only distance we can measure is zero. We always include this zero distance in our calculations, as it simplifies certain equations. With two points, we can derive two distances: the distance between them (d) and the zero distance.

As we increase the number of points to three, the possible distances depend on the arrangement of the points:

If the three points form an equilateral triangle, only two distinct distances are present: the length of a side and zero. However, if the three points form a scalene triangle, all sides can have different lengths, resulting in four distinct distances: 0, a, b, and c.

With the addition of more points, the number of possible distance combinations increases. However, our focus is on determining the minimum number of distinct distances that can be formed.

If we can establish this minimum, we can assert that n points will always generate at least that many distances. The maximum is less intriguing, as it simply reflects a scenario where every combination of points yields a unique distance, calculable by the formula (n(n-1)/2)+1.

To estimate the minimum number of distances, let’s consider perfect square numbers of points. By arranging four and nine points in the most symmetrical way—a grid—we find:

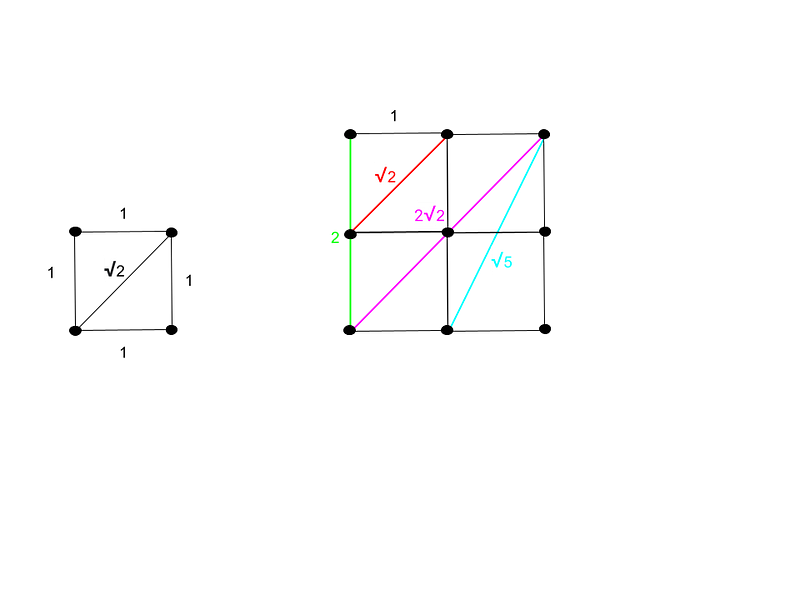
The minimum number of distances for four points is three, while for nine points, it is six. This leads us to define the Erdős Distance Problem more formally: How does the minimum number of distances increase as n, the number of points, becomes larger?

Chapter 2: Formulating the Conjecture

Erdős's conjecture is somewhat technical. At its essence, it posits that the number of distinct distances increases proportionally with n. Specifically, Erdős determined that when n is a perfect square, the minimum number of distances can be approximated by n/√(log n). This indicates that achieving fewer distances than this is not feasible.

To better understand the behavior of d(n)—the minimum number of distances formed by n points—we can plot values such as d(1)=1, d(2)=2, d(3)=2, d(4)=3, and d(9)=6, among others. Analyzing the growth rate of d(n) as n increases reveals that it trends upward and remains bounded between two linear functions after a certain point.

Notably, Erdős proved that d(n) must exceed √n, establishing that the minimum number of distances formed by n points is always greater than a constant multiple of √n.

Erdős's proof, delivered in 1946, employs a clever argument. Consider a set of n points, selecting one as a reference point (p). We can draw circles around p, each corresponding to the distance from p to the remaining points. If we denote the number of these circles as t, we can apply the Pigeonhole Principle to show that at least one circle must contain at least n/t points.

Continuing with this idea, if we draw a line through p that avoids intersecting any points, one segment must contain at least half of the n/t points, thus enabling us to identify distinct distances.

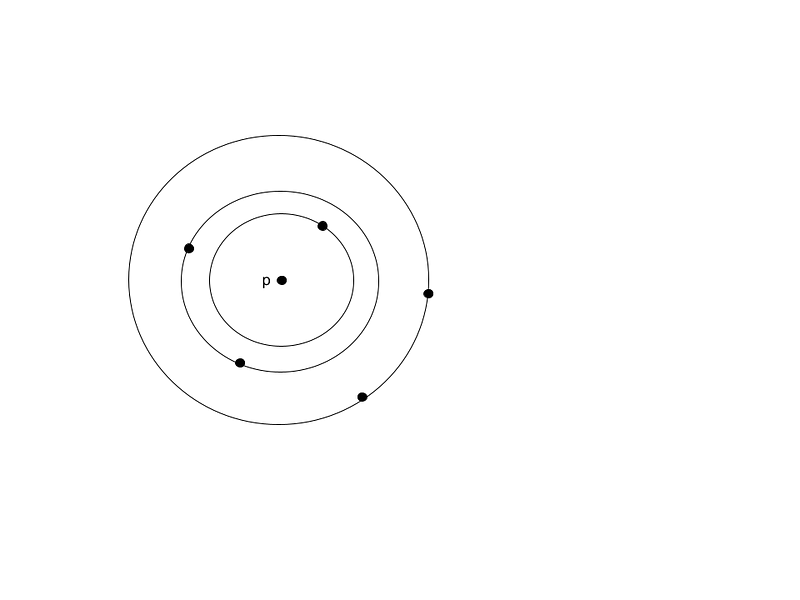
This argument leads us to conclude that the number of distinct distances exceeds the greater of t and n/(2t). Consequently, if t is less than n, we derive the inequality d(n) > n/(2√n) = (1/2)√n, affirming that at least (1/2)√n distinct distances must arise from n points.

Chapter 3: Progression and Future Directions

The journey to refine the understanding of the Erdős Distance Problem has yielded fascinating results over the decades. Initially, Moser established a lower bound of n^(2/3) in 1952, while Székely improved this to n^(4/5) in 1997. More recently, Solymosi and Tóth achieved n^(6/7) in 2001.

In 2015, a groundbreaking paper by Guth and Katz demonstrated that d(n) > Cn/(log n), effectively bringing the exponent down to 1.

As we have primarily focused on the two-dimensional plane, it is important to note that the Erdős Distance Problem extends into higher dimensions. Erdős conjectured that in d-dimensional space, n points must yield at least n^(2/d) distances.

For those seeking a deeper understanding of this problem, "The Erdős Distance Problem" by Garibaldi, Iosevich, and Senger serves as an excellent resource.

This video titled "Distance on a Number Line" offers a visual explanation of distance concepts that can further illuminate the principles discussed in this text.

Additionally, the video "How To Find The Distance Between Two Points" provides practical insights into distance calculation, complementing our exploration of the Erdős Distance Problem.