Understanding the Central Angle Theorem in Geometry
Written on
Chapter 1: The Basics of Central Angles
In geometry, the Central Angle Theorem states that a central angle subtended by an arc is twice the measure of any inscribed angle that intercepts the same arc. If your math instructor were to initiate a discussion about this theorem, would you bring up Thales' theorem? If so, a response might be, “Yes, but only partially.” This is because the arc related to the inscribed angle can either be part of a semicircle or have a major or minor length. The semicircle case is specifically referred to as Thales' theorem. We will begin with this explanation, but first, let’s clarify some key definitions.
Definitions:
- Vertex: The point where two lines intersect.
- Diameter: A straight line segment that runs through the center of a circle, connecting two points on the circle. There are infinitely many diameters possible.
- Chord: A straight line segment that connects any two points on a circle, with the diameter being the longest chord.
- Arc: A section of the circumference of a circle.
- Central angle: The angle formed at the center of the circle by two radii.
- Inscribed angle: The angle formed by two chords in a circle which share an endpoint.
The first video titled "Central Angle Theorem" provides a comprehensive overview of the theorem, illustrating its significance and applications.
The Thales Theorem and the Semicircle
When a diameter bisects a circle, the central angle corresponding to the semicircle arc measures 180°. Consequently, any inscribed angle that has its endpoints at the diameter’s endpoints should measure half of that, resulting in a 90° angle. This forms a right triangle, with the diameter acting as the hypotenuse.
Let’s denote the endpoints of the diameter as A and A’, their angles as ? and ?’, and the vertex of the inscribed angle as B. By connecting these points, we create a triangle, which is indeed a right triangle due to the right inscribed angle, with the diameter as its hypotenuse.
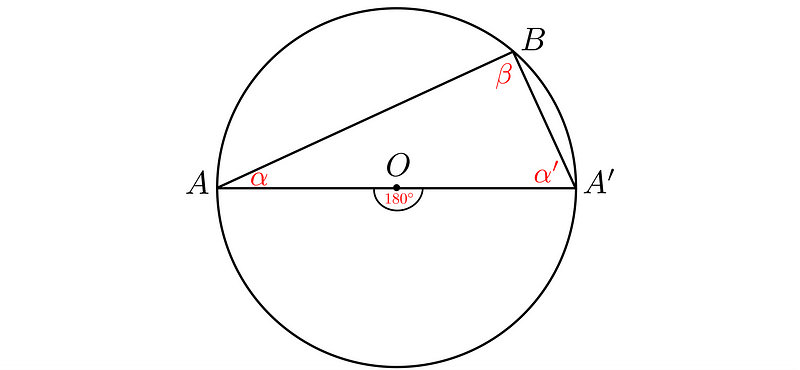
Ready to prove this essential theorem? Let's delve into the geometrical proof.
Geometric Proof of the Theorem
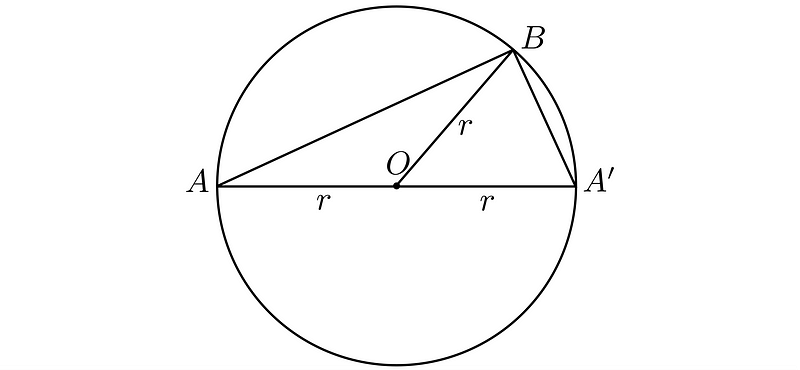
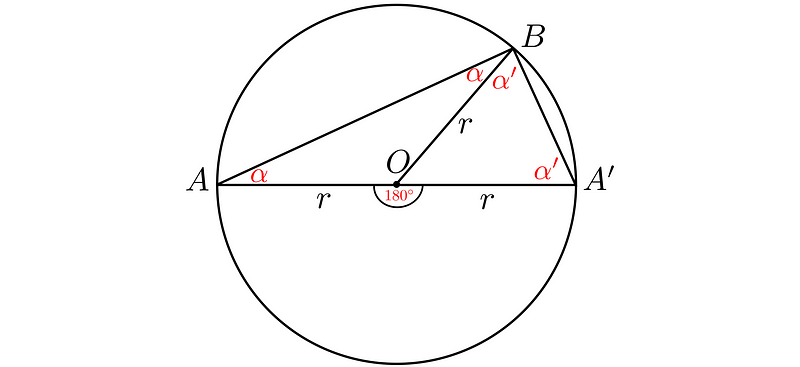
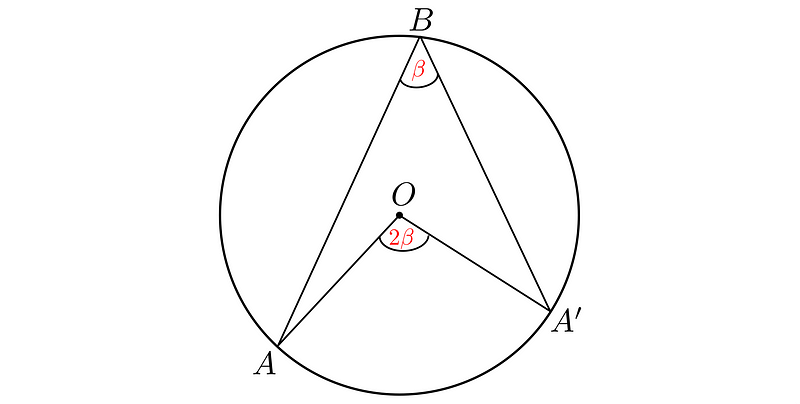
Observe that the segments connecting the circle's center O to the vertices are the radii. These divide the triangle formed by A, A’, and B into two isosceles triangles, as each triangle has two equal sides that correspond to the radius of the circle.
Both angles formed between the radii and the third side must be equal, thus we have ß = ? + ?’.
We also know that the sum of angles in any triangle is 180°. Therefore, summing the angles in triangle AA’B gives us:
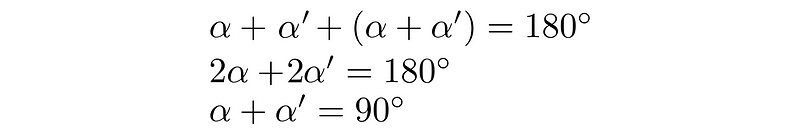
Thus, ß is indeed a right angle.
q.e.d.
The Pythagorean Proof (A Fun Twist)
Initially titled "The Pythagorean Proof", this section is enriched with insights that make it even more enjoyable to explore.
Assuming the inscribed angle ?ABA’ is half the measure of the central angle and is a right angle, we can utilize the Pythagorean theorem.
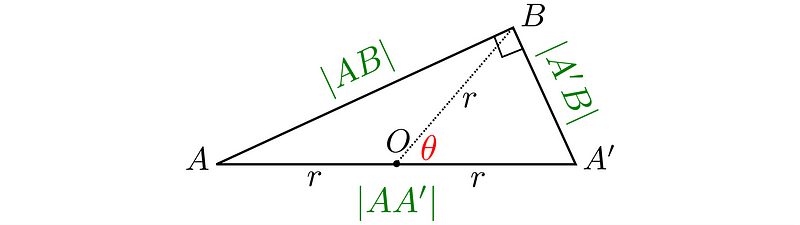
Don’t fret about angle ?; it will be clarified shortly. First, let’s apply the theorem to verify our claim.
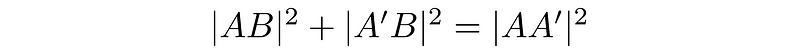
This angle ? simply represents the tilt of a line from the origin.
Now that we understand this, we can break down our line into components along the axes. Utilizing trigonometry allows us to compute these components, referred to as polar coordinates.
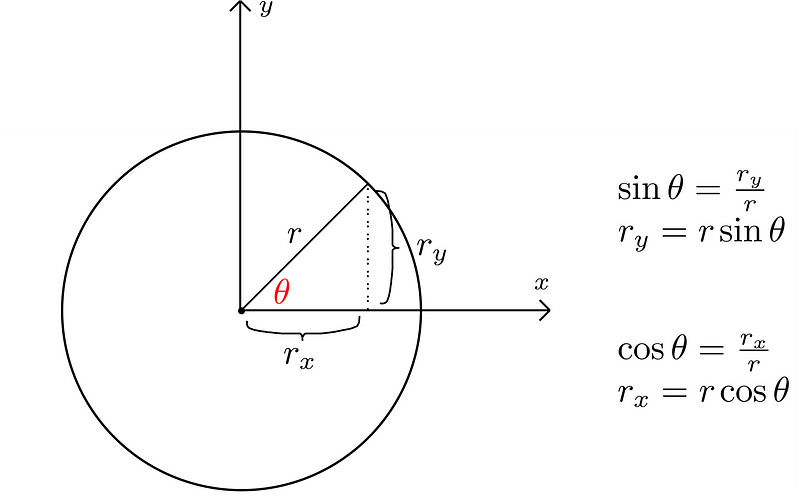
Returning to the proof, we need to resolve the sides along the right angle into x and y components, then apply the Pythagorean theorem to combine their lengths.
The length of AB is represented as follows:
Note that the x-component is the sum of r and r × cos?. The y-component consists of a single value.
The length of A’B is depicted as:
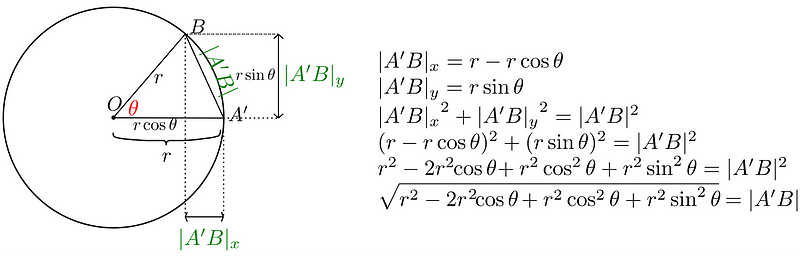
It's important to note that the x-component length here requires subtracting r × cos? from r. Interestingly, the y-components are equal, which is to be expected.
Now we can return to our initial formula, substitute these values, and verify the equality of the sides.
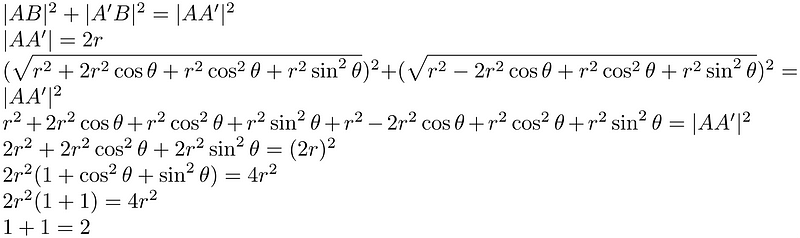
As we can see, everything checks out— and it should!
q.e.d.
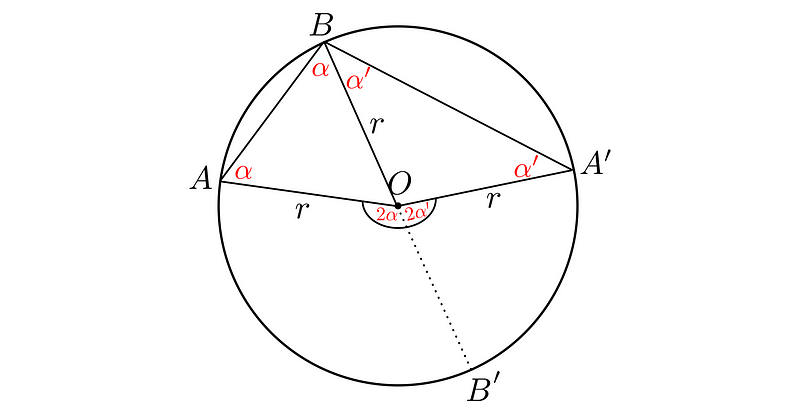
Major Arc (>180°)
In cases where the central angle exceeds 180°, the scenario differs from that of Thales. The radii do not form a diameter in this situation, resulting in a larger central angle. If the theorem still applies, then any inscribed angle should measure less than half of the central angle, thus exceeding 90°.
It looks like this:
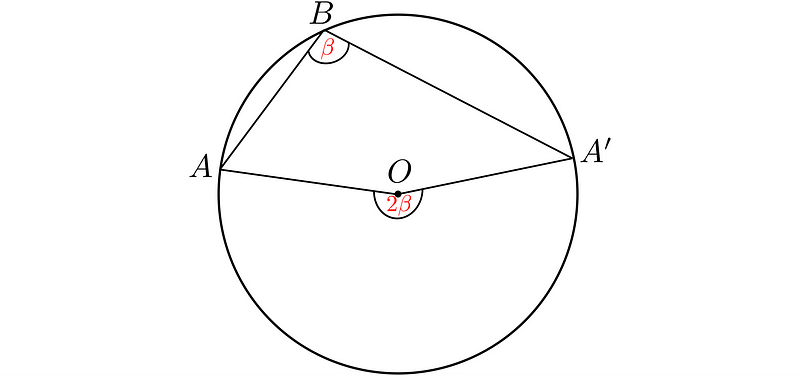
Geometric Proof
To prove this (and the following) case, three elements are necessary. Two are already familiar: the segments from the circle's center to each vertex are radii, which divide the figure into two isosceles triangles. But what is the third?
By reflecting the line OB around the perpendicular axis, we note the opposite point on the circle as B’. This creates a diameter.
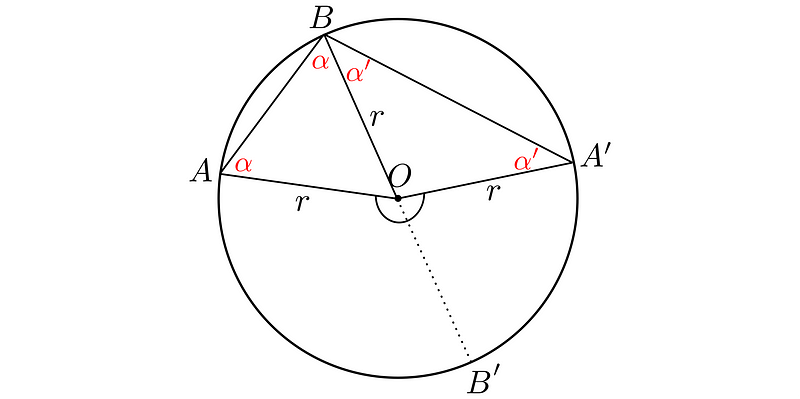
Now, if we draw an additional chord from B’ to each A and A’, we can analyze the situation as two separate cases: left and right. Both can be examined using Thales' theorem since BB’ serves as the diameter, the central angle equals 180°, and the inscribed angles ?BAB’ and ?BA’B’ are both 90°. As a result, ABB’ and A’BB’ form right triangles.
The left triangle appears as follows:
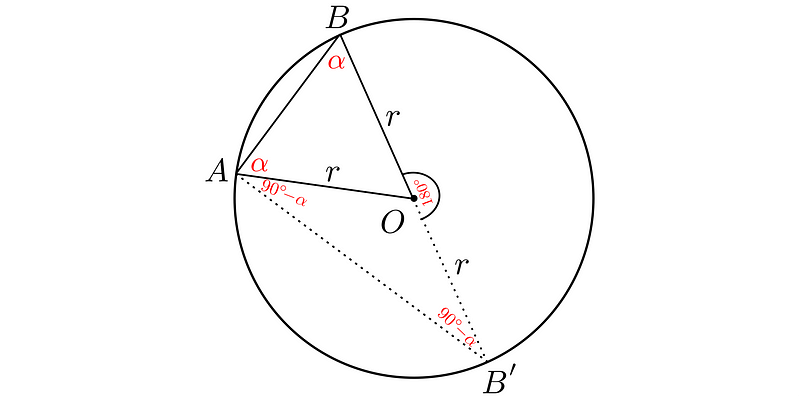
Determining the angle ?AOB’ will provide the value of the left part of the central angle. The angle ?BAB’ is 90°, and since its upper part is ?, the lower part must be 90° - ?. Consequently, the angle ?AB’O must be identical. By summing the angles in the lower triangle, we arrive at:
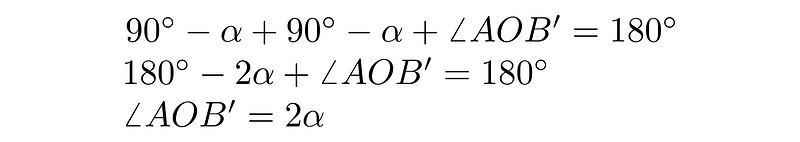
Thus, the left section of the central angle is indeed twice the size of ?.
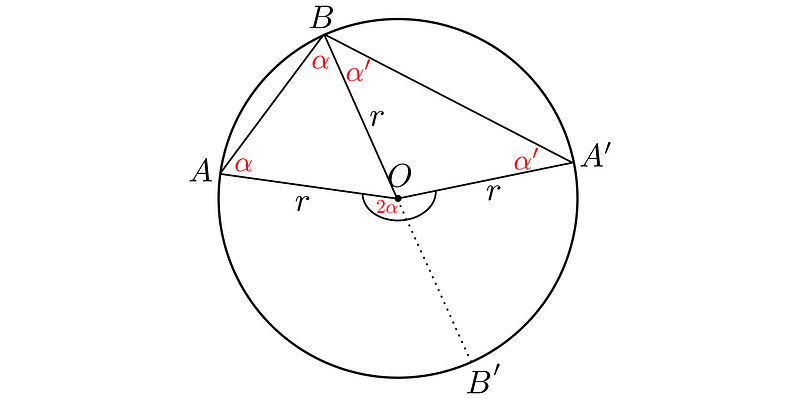
The right section is similarly analyzed:
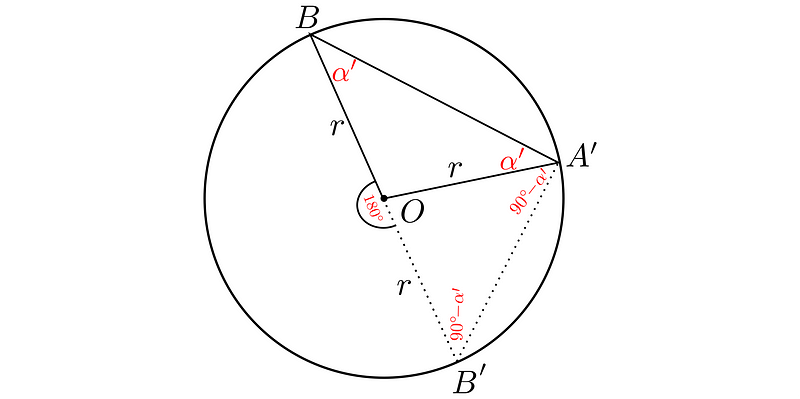
We repeat the same process as with the left side, obtaining:
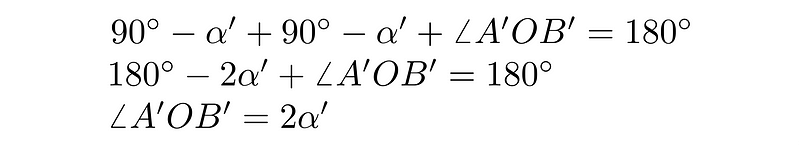
Thus, it is confirmed that the central angle is indeed twice any inscribed angle subtended by the same arc.
q.e.d.
Minor Arc (<180°)
Finally, when the central angle is less than 180°, the steps mirror those of the major arc case, albeit with a different configuration.
Geometric Proof
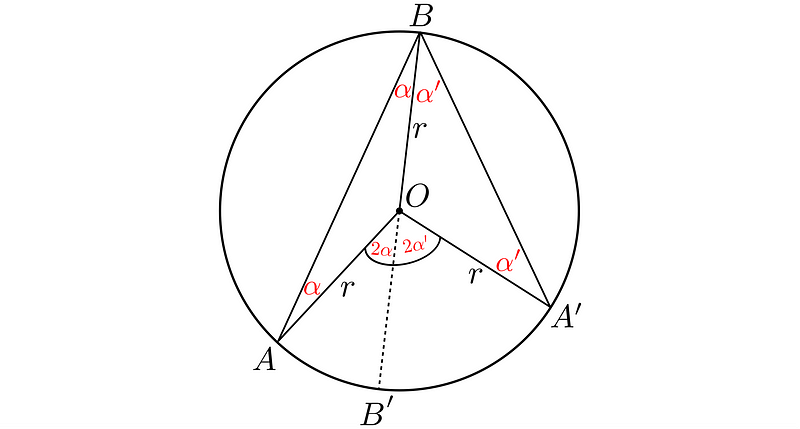
To address this, we again draw the BB’ diameter, which will split our problem into a left and a right segment.
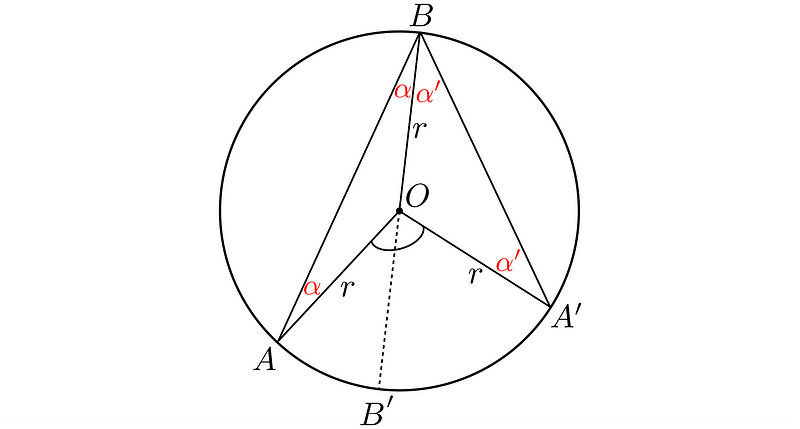
The left section is represented as follows:
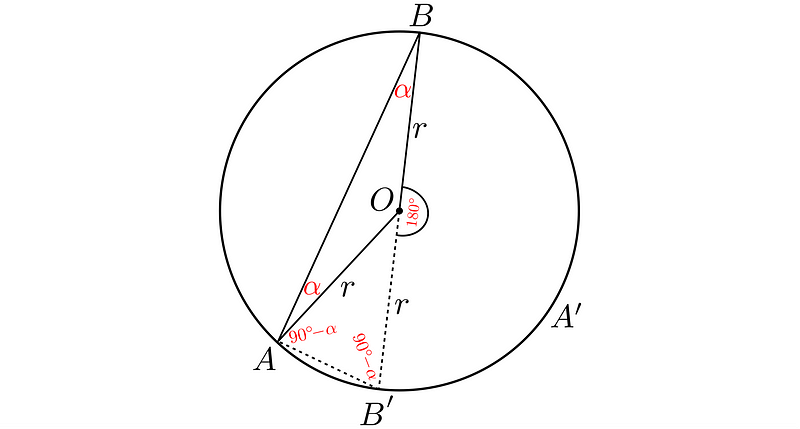
Here, the angle ?BAB’ is 90°, and its upper section is ?. Thus, the lower segment must be 90° - ?. The angle ?AB’O must also be identical. Summing the angles in the lower triangle yields:
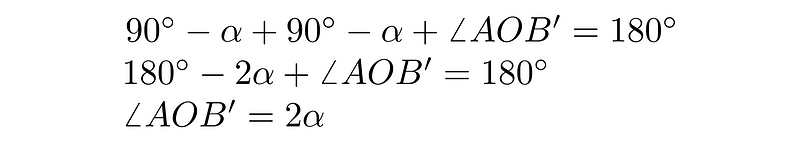
After applying the situation, we can write:
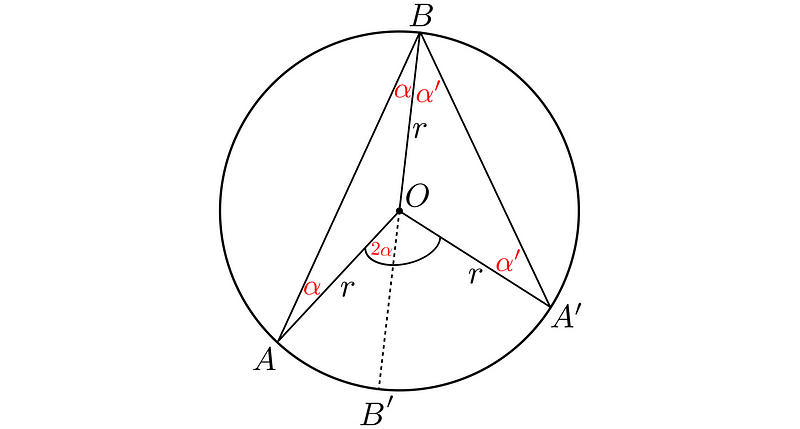
The right side:
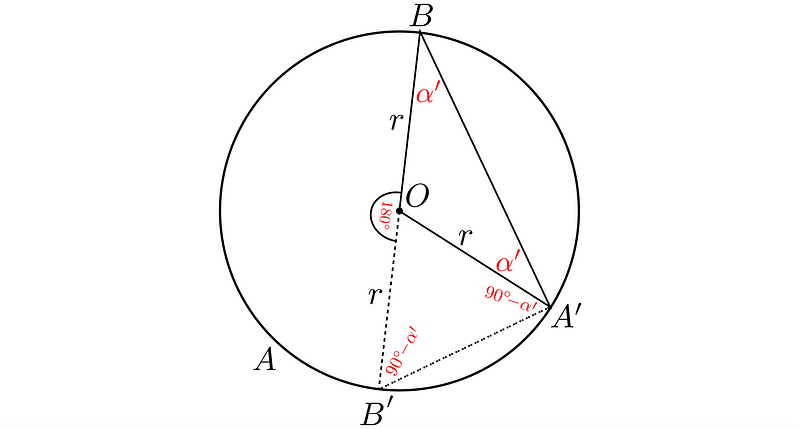
Once again, the inscribed angle ?BA’B’ is 90°. Since its upper part is ?’, the lower must equal 90° - ?’. The angle ?A’B’O shares the same measure. Summing the angles in the lower triangle gives us:
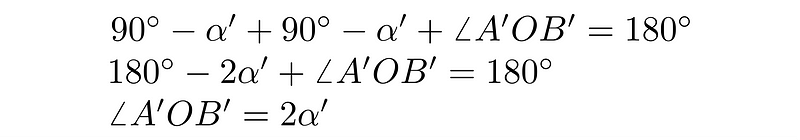
This results in:
Thus, we confirm that the Central Angle Theorem holds true in this case as well.
q.e.d.