Old Approaches to Quantum Mechanics

Matrix mechanics, introduced by German physicist Werner Heisenberg in 1925, marked the first successful attempt to quantize atomic spectra. In the same year, Austrian-Irish physicist Erwin Schrödinger developed wave mechanics, proving their equivalence a year later. The contemporary understanding of quantum mechanics, where states are represented as mathematical constructs in Hilbert space, is largely credited to English physicist Paul Dirac. The evolution of quantum field theory led to the creation of various formulations of quantum mechanics.

Among these formulations is the path integral approach, which generalizes the action principle from classical mechanics. This framework posits that the quantum transition between two states arises from evaluating a functional integral over all conceivable classical trajectories. Thus, it replaces the classical idea of a single trajectory with a comprehensive summation of potential paths. Although other scientists, including Norbert Wiener and Paul Dirac, contributed to this formulation, Feynman fully developed the method in 1948.

Feynman's article, “Space-Time Approach to Non-Relativistic Quantum Mechanics,” states:

“[Q]uantum mechanics is formulated here in a different way. It is, however, mathematically equivalent to the familiar formulation... The probability that a particle will be found to have a path x(t) lying within a region of spacetime is the square of a sum of contributions... The total contribution from all paths reaching x, t from the past is the wave function ?(x, t). This is shown to satisfy Schrödinger’s equation...”

To begin, let’s explore the concept of a quantum propagator.

Quantum Propagators

In quantum mechanics and quantum field theory, propagators are functions that determine the probability amplitude for a particle's transition between positions over a given time interval. The square of this amplitude yields the transition probability.

Let <b>X</b>(<i>t</i>) denote the time-dependent position operator in the Heisenberg picture. Utilizing Dirac’s bra-ket notation, we can consider the following initial and final state vectors:

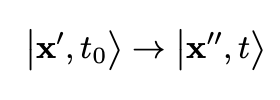
These vectors are eigenstates of the operator <b>X</b>(<i>t</i>). The propagator corresponding to the transition is represented by:

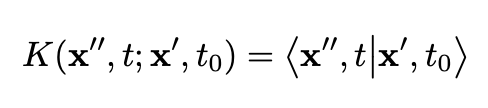
This function denotes a transition amplitude.

Completeness of the Set of Position Kets

The probability of obtaining <i>any</i> result when measuring the position of a system at a fixed time must equal 1, which implies that position kets form a complete set:

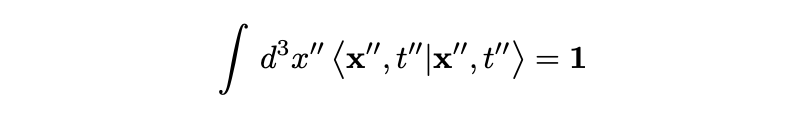
The unit on the right-hand side represents the identity operator. This relationship can be used to express the propagator as a series of integrals, allowing us to represent a transition as a combination of intermediary transitions. The simplest scenario is:

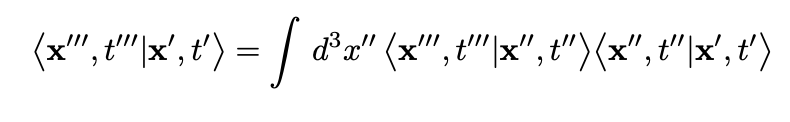
Using the compositional property of the propagator, we can partition the time interval for a transition between two states:

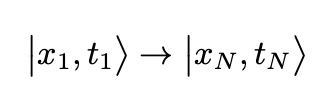
into equal segments of length:

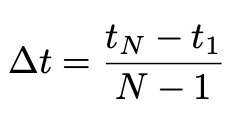
and express the transition amplitude as a composition of amplitudes:

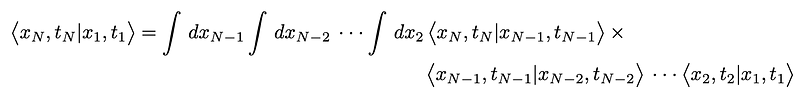
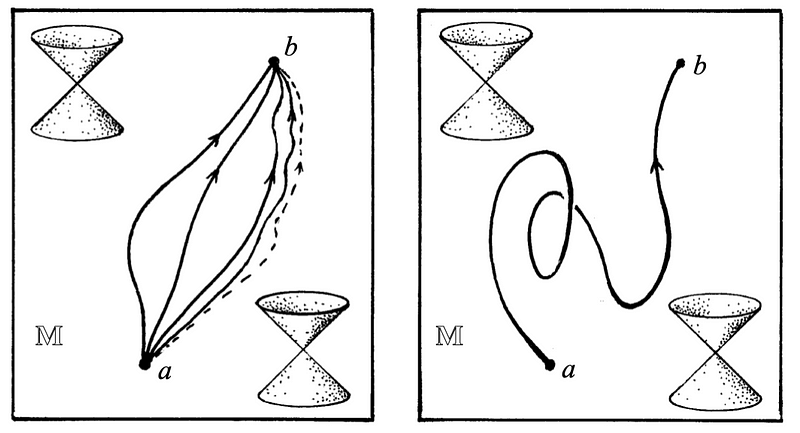
This process involves summing over all possible paths with fixed endpoints, as illustrated in the accompanying figure.

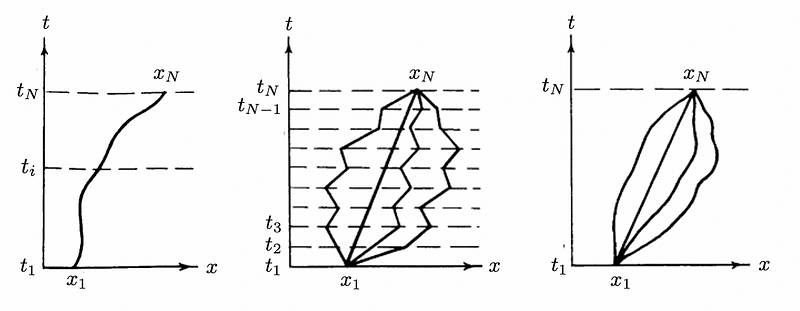
The leftmost diagram depicts the unique path characteristic of classical mechanics. To derive this path, consider a particle with an associated Lagrangian <i>L</i>(<i>x</i>, <i>dx</i>/<i>dt</i>). The path is identified by extremizing the action:

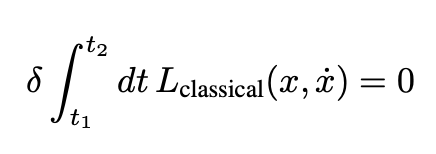
This principle is known as Hamilton’s principle.

Feynman’s Space-Time Approach

In contrast to classical physics, which considers a particle's motion to follow a specific trajectory, quantum mechanics necessitates accounting for all possible paths. The challenge lies in demonstrating that quantum mechanics converges with classical mechanics as <i>h</i>? 0.

In a 1933 paper, Paul Dirac made an enigmatic remark that perplexed Feynman. Adapting the notation per Sakurai, Dirac stated:

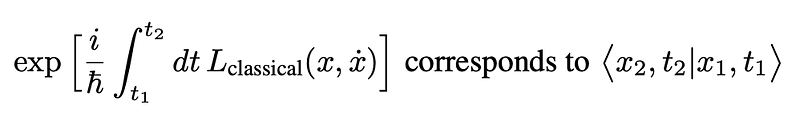
Feynman’s curiosity about the meaning behind Dirac's words motivated him to develop his influential space-time framework for quantum mechanics.

According to Sakurai, the action for a small segment of the path is expressed as:

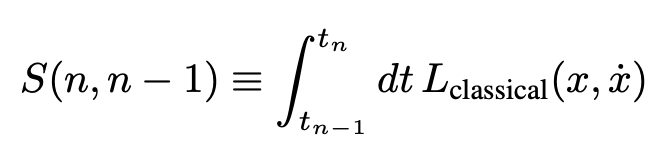
The corresponding amplitude for a given path is obtained by multiplying these expressions. The propagator for the transition can then be calculated by summing over all possible paths:

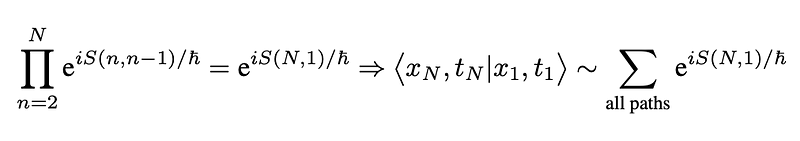
For small <i>h</i>, the predominant term in this summation corresponds to a path that remains stable under slight deformation, since the contributions from other paths cancel out due to the rapid oscillation of the exponentials. This implies that this path satisfies:

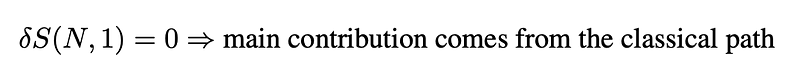
Consequently, according to Hamilton’s principle, the amplitude depends only on the classical path, confirming that classical mechanics is indeed recovered when <i>h</i> is small.

Feynman reformulated Dirac’s expression as a proportionality:

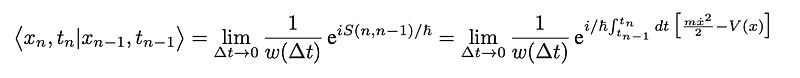
In James Gleick's biography of Feynman, he recounts an intriguing exchange between Feynman and Dirac:

“Feynman looked out the window and saw Dirac... He had a question that he had wanted to ask Dirac since before the war... A remark in a 1933 paper of Dirac’s had given Feynman a crucial clue... Dirac had written, but neither he nor anyone else had pursued this clue until Feynman discovered that the ‘[corresponds]’ was, in fact, exactly proportional... ‘Are they?’ Dirac asked. Feynman said yes, they were. After a silence, Dirac walked away.”

Setting <i>V</i> = 0 for simplicity, employing a linear approximation for <i>S</i>(<i>n</i>, <i>n</i>-1), and integrating both sides of the proportionality leads to the prefactor 1/<i>w</i>(?<i>t</i>):

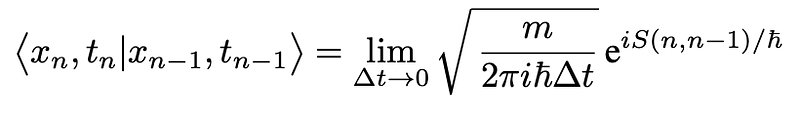
The transition amplitude for the entire path is derived by integrating over all intermediate stages:

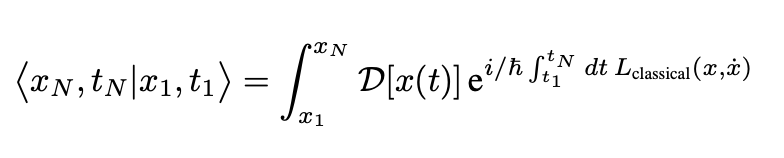
with:

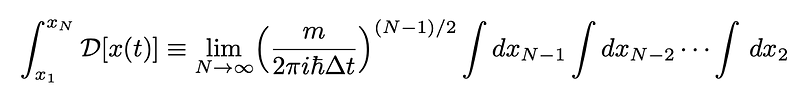
This represents what is known as Feynman’s path integral, encompassing the summation (or integral) of all potential trajectories. The associated diagram can be found in the previous figures.

It is essential to recognize that, unlike other quantum mechanics formulations, the probability amplitude is not merely a linear complex combination of quantum states. Instead, it reflects a quantum superposition of entire alternative histories in spacetime. The notion here is that quantum mechanically, there exists a complex superposition of “alternative realities.” However, the exponential weighting, often referred to as amplitude,

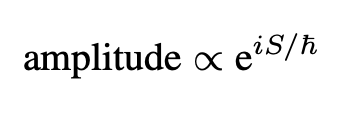
is, in reality, an “amplitude density,” as we must integrate over the infinite space of classical alternatives, resulting in an infinite-dimensional space that presents complex behavior.

Moreover, it is crucial to note that the trajectories are not constrained by the principles of special relativity; any trajectory is permissible provided the endpoints are fixed. This scenario is illustrated in the following figure.

Equivalence of Feynman’s and Schrödinger’s Approach: A Proof

We will now demonstrate that Feynman’s approach aligns with Schrödinger's wave mechanics. We start by expressing:

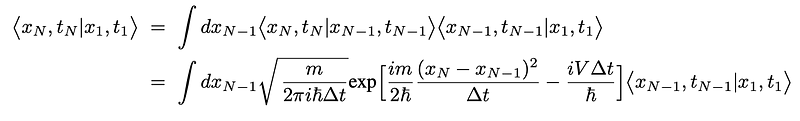
where we assume:

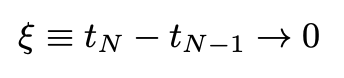
Renaming the final position and time as <i>x</i> and <i>t</i> + ?<i>t</i>, employing <i>?</i> in the earlier equation, and expanding the exponential and the amplitude within the integral in powers of <i>?</i>, we can collect terms and perform straightforward Gaussian integrals to yield:

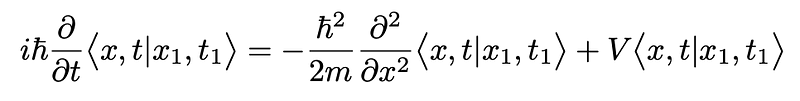
We conclude that both Feynman’s and Schrödinger’s propagators (from his wave mechanics) are equivalent!

Thank you for reading, and I look forward to your feedback! For more intriguing content on physics, mathematics, machine learning, deep learning, finance, and beyond, feel free to check out my LinkedIn, personal website at www.marcotavora.me, and GitHub!