Superrationality: Exploring Decision Theory and Its Implications
Written on
Chapter 1: Understanding Functional Decision Theory
In the preceding chapter, we examined how PLAYER, a computer program, effectively tackled both Newcomb’s Problem and the Smoking Lesion scenario by asking: “Which output from PLAYER leads to the most favorable outcome?”
This approach aligns with Functional Decision Theory (FDT). While Causal Decision Theory (CDT) inquires about which action yields the best result, and Evidential Decision Theory (EDT) looks for the action that serves as the best indicator of a positive outcome, FDT poses a different question:
What output from this decision-making process results in the optimal outcome?
Within the computational realm discussed in Chapter V, it’s clear that PLAYER should opt for one-boxing. However, how does FDT guide our decisions in the real world?
When Carl, Eve, and their peers engaged with Newcomb’s Problem in Chapter I, it became apparent that Omega was simulating their decision-making process to inform her predictions.
What does it mean to simulate a decision-making process?
To clarify, PLAYER operated using a function: it received an input (for instance, Newcomb’s Problem) and generated a predetermined output (one-box or two-box) for that input. Omega could replicate this function (by executing PLAYER) to formulate her predictions.
Carl, Eve, and their companions, unlike PLAYER, are not computer programs; however, they possess their own method for decision-making within Newcomb’s Problem. Thus, they too execute a function, which we refer to as a decision-making procedure.
When Omega forecasts Carl’s actions, she simulates Carl’s decision-making process—essentially calculating the function that Carl’s procedure implements. The output of this function indicates a tendency to two-box, as Carl consistently opts for that choice. Consequently, Omega predicts Carl will two-box, leading her to place an empty envelope in Box B.
So, what does FDT ultimately advise?
One-boxing!
But why is that the case? In the computational scenario, we were concerned with how to program PLAYER to achieve the best outcome beforehand. In real life, however, you decide whether to one-box or two-box after Omega has made her prediction!
That’s true, but Omega also considers the same function as you before she makes her prediction!
Yet, we cannot alter the past!
Indeed! It might seem like I’m suggesting we can, but bear with me.
Two Calculators
To illustrate this concept, let’s use an analogy. Imagine John and Mike each possess identical calculators.
On Tuesday, John inputs 65 x 76 into his calculator and records the answer without telling Mike.
On Wednesday, Mike enters the same calculation into his calculator and sees the result: 4940. He then approaches John, who confirms he had calculated 65 x 76 the previous day.
Does Mike need to inquire about John’s calculator's result?
Clearly, the answer is no. Mike understands that John’s calculator produced the same output as his own: 4940.
Mike is aware of this because both calculators are executing the same function (the multiplication function) with identical inputs—65 and 76.
Thus, since the multiplication function (like all functions) yields a single output for any specific input pair, Mike is confident that John’s calculator must have generated the same result.
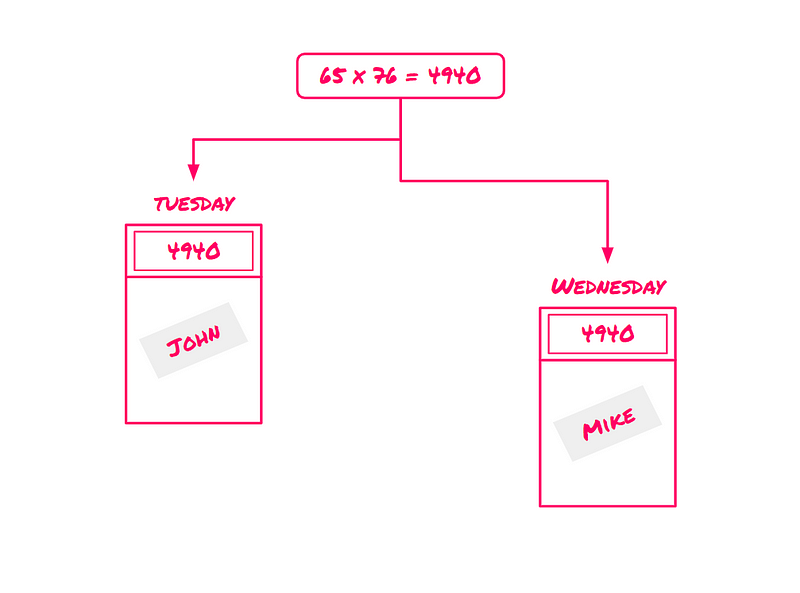
John’s calculator produced the same answer as Mike’s for the input 65 x 76 on different days.
No one finds this hypothetical scenario surprising. No one believes Mike’s calculator influenced John’s calculator to yield “4940.”
So why be astonished when one-boxing means Omega predicted you would one-box? One-boxing does not cause Omega to forecast a one-boxing outcome any more than Mike’s calculator affected John’s calculator’s output of “4940.” It’s simply that if you choose to one-box, you are aware Omega anticipated your decision.
Subjunctive Dependence
Both John and Mike’s calculators implement the multiplication function. Generally, when two systems (such as calculators, computers, humans, or Omega) execute the same function, they are subjunctively dependent upon that function.
Subjunctive dependence explains why it is not surprising that both calculators returned 4940. It also clarifies why Omega predicts you will one-box if you indeed decide to one-box.
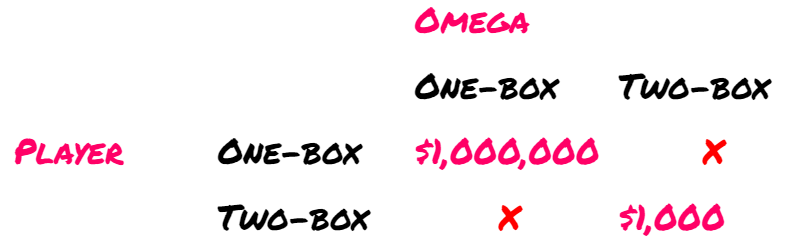
According to FDT, there are only two potential outcomes in Newcomb’s Problem.
Yet, it feels as though the second scenario involves altering the past, while the first does not (at least, that’s my perception at times). It seems that when Omega has predicted you will one-box, you still have the option to two-box (and potentially receive $1,001,000!).
Ultimately, you retain the ability to make any choice you desire. However, that choice has already been predicted!
Now, some might argue that human behavior isn’t as predictable. Omega may not effectively model your decision-making process!
That is a valid viewpoint. While I may not concur, I can understand why some readers might feel this way.
Let’s say Omega does not model your decision-making at all. Imagine that everyone wearing a hat one-boxes while those without hats two-box. In this case, Omega makes her prediction by simply checking your hat status.
Note that there is now no subjunctive dependence between you and Omega! Your decision-making occurs solely in your mind, independent of Omega’s calculations, and does not affect Box B’s contents.
Thus, we find ourselves in a situation akin to Smoking Lesion!

The distinction between these two scenarios lies solely in the presence or absence of subjunctive dependence. Consequently, FDT now advises two-boxing!
It’s important to note that in upcoming discussions, I will explicitly assume subjunctive dependence. However, it’s essential to recognize that FDT does not automatically presume its existence; ideally, a decision-maker following FDT should identify subjunctive dependence only when it is present and act accordingly.
Chapter 2: The Psychological Twin Prisoner’s Dilemma
You and your accomplice have been detained for two offenses: a minor burglary and an armed robbery. The authorities possess enough evidence to convict you both for the burglary but lack sufficient evidence for the robbery.
As a result, the police devise a strategy. They separate you into different rooms—preventing any communication between you—and present both of you with the same offer:
If you testify against (betray) your partner, you will face no penalties for the burglary.
If only one of you betrays the other, the betrayer walks away free while the betrayed partner receives a 5-year sentence (4 years for the robbery and 1 year for the burglary).
If both of you betray one another, you each serve 4 years for the robbery.
Finally, if both remain silent, you each receive 1 year for the burglary.
Interestingly, both you and your partner are aware that you share the same decision-making procedure for resolving this dilemma. To maximize your chances of getting out sooner, should you betray your partner or remain silent?
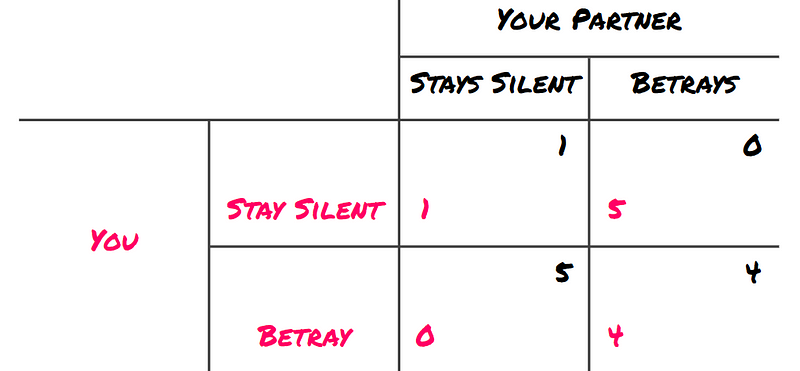
If your partner betrays you, retaliating will result in one year less in prison than choosing to stay silent. Conversely, if your partner remains silent, the same logic applies!
Eve would argue that betraying your partner suggests that your partner will betray you as well. Hence, she opts to remain silent.
On the other hand, Carl believes that since you cannot communicate, your actions do not affect your partner’s choice in this situation. As betraying his partner results in a shorter prison term regardless of her actions, he chooses to betray her.
Now, what about Fiona, who adheres to FDT?
In her view, whatever you decide, your partner will do the same. You both are subjunctively dependent on each other’s decision-making processes! Achieving freedom immediately isn't feasible—it necessitates differing decisions from both parties!
Thus, you will either both betray each other or both choose to remain silent. The latter option allows you to gain freedom 3 years earlier. Therefore, Fiona decides to stay silent.
It’s worth noting that in this dilemma, you and your partner make your decisions simultaneously. However, this detail is not crucial to the problem! The essence remains unchanged if your partner decides a day earlier. Subjunctive dependence transcends time.
Moreover, the Psychological Twin Prisoner’s Dilemma bears a striking resemblance to Newcomb’s Problem upon closer inspection:
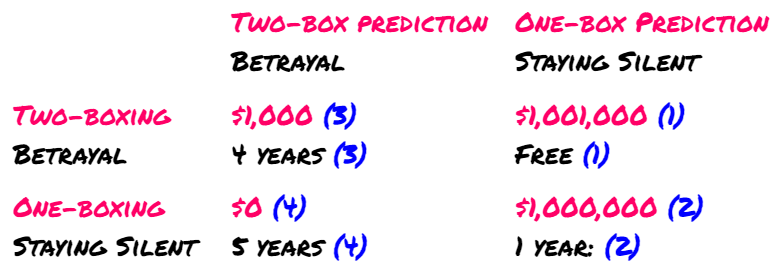
When comparing the Psychological Twin Prisoner’s Dilemma to Newcomb’s Problem, notice the order of preferred outcomes (highlighted in blue) remains consistent across both scenarios. Additionally, in both cases, options (1) and (4) are unattainable due to subjunctive dependence.
Subjunctive dependence may still seem enigmatic, but I hope it will become clearer in Chapter VII. Thank you for reading!
If you wish to support Street Science, consider contributing on Patreon.
The video titled "What Were You Thinking? Decision Theory as Coherence Test" by Prof. Itzhak Gilboa delves into the nuances of decision theory and its implications in various dilemmas, enhancing the understanding of functional decision-making processes.