# Can You Actually Fold a Piece of Paper More Than Seven Times?
Written on
Chapter 1: The Seven Fold Myth
We've all encountered someone who claims that a piece of paper can only be folded in half seven times. Back in my school days, I decided to test this theory. I took a piece of paper and began folding it: once, twice, and so on, until I reached the seventh fold. At that point, despite our best efforts—standing on it, using weights, and even slamming it in a door—we couldn’t manage an eighth fold. Meanwhile, the friend who instigated this challenge watched with amusement, presumably envisioning a future Nobel Prize for his "scientific" claim.
I accepted this notion as fact until my sophomore year at university, when a mathematics professor introduced us to the "bedsheet problem." He mentioned Britney Gallivan, who in 2002 achieved the incredible feat of folding a large sheet of paper twelve times, earning her a spot in the Guinness Book of World Records. This revelation shattered my belief and introduced me to another Britney beyond the famous pop star.
Instead of simply folding the paper in half repeatedly, Gallivan approached the problem differently. This reflects a vital principle in mathematics: when one method fails, it's often wise to explore alternative solutions.
Before we delve into the specifics of how Gallivan accomplished her record, let’s first understand why folding paper becomes increasingly difficult with each attempt.
Section 1.1: The Challenge of Folding Paper
Folding paper itself isn’t particularly challenging; however, the difficulty escalates with each fold. This occurs because, as you fold the paper, it becomes thicker and more resistant to further folds. This phenomenon is an example of exponential growth. To illustrate, let’s consider a standard notebook paper with a thickness of 0.01 cm. After one fold, it measures 0.02 cm, and after six more folds, the thickness progresses as follows: 0.04 cm, 0.08 cm, 0.16 cm, 0.32 cm, 0.64 cm. By the seventh fold, the paper's thickness has increased nearly 128 times its original measurement.
You might argue that folding a notebook with 128 pages is easy, but remember, that piece of paper has become significantly thicker and its area too small to apply the necessary force for folding.
Can someone with extraordinary strength fold the paper more than seven times? Yes, it is possible. If the paper remains intact, individuals have successfully folded it eight, nine, or even twelve times.
You may wonder why no one has folded paper more than twelve times. The answer lies again in exponential growth. After seven folds, the paper is 0.64 cm thick. Continuing this process, we find the thickness after each additional fold as follows: 1.28 cm, 2.56 cm, 5.12 cm, 10.24 cm, and 20.48 cm—equivalent to the width of an exceptionally thick book.
To visualize, if we attempted to fold paper that is 20.48 cm thick, we would need a piece as large as a football field. While theoretically plausible, no one is likely to create such a massive sheet of paper for this purpose.
Folding paper is not only an amusing brain teaser but also an engaging way to illustrate exponential growth. For instance, after twelve folds, the paper measures 20.48 cm. Continuing this pattern reveals astounding thicknesses as follows:
- Fold 13: 40.96 cm
- Fold 14: 81.92 cm
- Fold 15: 163.84 cm
- Fold 16: 327.68 cm
- Fold 17: 655.36 cm (6.55 meters)
- Fold 18: 1310.72 cm (13.1 meters)
- Fold 19: 2621.44 cm (26.2 meters)
- Fold 20: 5242.88 cm (52.4 meters)
- Fold 21: 10485.76 cm (104.8 meters)
- Fold 22: 20971.52 cm (209.7 meters)
- Fold 23: 41943.04 cm (419.4 meters)
- Fold 24: 83886.08 cm (838.9 meters)
- Fold 25: 167772.16 cm (1.7 km)
- Fold 26: 335544.32 cm (3.4 km)
- Fold 27: 671088.64 cm (6.7 km)
- Fold 28: 1342177.28 cm (13.4 km)
- Fold 29: 2684354.56 cm (26.8 km)
- Fold 30: 10737418.24 cm (107.3 km)
If you follow this pattern, by fold 42, you could theoretically reach the moon, and by fold 51, the sun—though the paper would burn long before that. Hypothetically, if one could fold paper infinitely, at fold 81, it would reach 127.786 light-years in thickness, an incomprehensible distance.
Section 1.2: The Mathematics Behind Folding Paper
Folding paper lacks a universal theorem, much like the debate over who gets wetter in the rain, the runner or the walker. To solve the folding dilemma, we must consider numerous variables: paper thickness, size, material, manufacturing process, and the risk of tearing.
So how did the myth that paper can only be folded seven times become prevalent? It largely stems from the common use of A4 paper. Yes, if confined to A4 dimensions, the maximum folds achievable before requiring excessive force is seven. Even then, tearing becomes a significant concern.
However, not all paper is limited to this constraint. With larger sheets and the right conditions, more folds are achievable. Despite the absence of a universal theorem, we can derive an equation for this phenomenon. This was achieved by Britney Gallivan, a high school student.

In 2002, during an Honors Pre-Calculus class, Gallivan's teacher challenged the students to explore the folding limits. Initially encountering the seven-fold barrier, she understood that a larger piece of paper was essential. She then set out to derive an equation to quantify the required size for multiple folds.
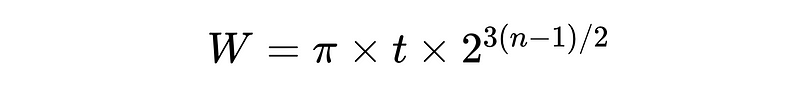
In her formula, n represents the number of folds, and t denotes the paper's thickness. By substituting real values for n and t, W calculates the length of paper required to achieve the desired folds. For instance, folding a 0.01 cm thick sheet twelve times necessitates a piece measuring 29.12 meters. However, the practicality of such dimensions is questionable due to the high likelihood of tearing.
Gallivan later devised a more sensible equation, accounting for both paper length and thickness, which allowed her to fold the paper in the same direction each time.
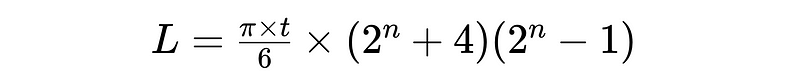
Despite this new approach minimizing tearing, she still required a length of 880 meters for her experiment. Lacking such a piece, Gallivan ingeniously employed toilet paper. By attaching six rolls together, she created the necessary length and successfully folded it twelve times.
Gallivan's determination led her to walk considerable distances for each fold, eventually shortening the distance with each iteration. By the twelfth fold, her task became significantly easier.
In conclusion, I commend Britney Gallivan not merely for breaking a record but for her relentless pursuit of knowledge and understanding when faced with a challenge.
Note 1: Subscribe to Beyond Euclid! for high-quality math and science content delivered weekly.
Note 2: I may earn commissions from purchases made through affiliate links in this post.